о глубинной математике

[Око]

Алгебра Ли - это математический объект, представляющий собой векторное пространство с определенной операцией, называемой скобкой Ли (или коммутатором), удовлетворяющей определенным свойствам.
группа Ли Е8, 248 измерений. самая сложная группа.
(подробно о свойствах групп Ли - https://habr.com/ru/articles/117287/)

решетка группы Е8

Математикам потребовалось четыре года, чтобы с помощью суперкомпьютера построить и создать это двухмерное представление трехмерного представления четырехмерной проекции непостижимой проекции 8 измерений с ее 248 пересечениями или вершинами.
Благодаря различным проекциям можно увидеть, что вершины расположены в трёх основных кольцах по 72. во внешнем кольце 12 вершины (по каждому знаку зодиака).

Добавлено спустя 2 минуты 50 секунд:

Группа Е8 описывает симметрии в пространстве, имеющем 57 измерений, что очень необычно для людей, привыкших к трехмерному пространству. Хотя эта группа была известна уже давно, сейчас ученые полагают, что она может быть связана со структурой вселенной.

В своем исследовании команда математиков-теоретиков использовала сложные методы программирования, чтобы составить описание объекта E8. Полная информация о нем сейчас содержится в файлах объемом в 60 гигабайт. Этого объема было бы, например, достаточно, чтобы хранить файлы с музыкой в формате MP3 для непрерывного проигрывания их в течение 45 дней. Эти вычисления потребовали новых сложных математических методов, не доступных еще несколько лет назад.

Ученые Института математики (American Institute of Mathematics) считают, что этот результат окажет такие последствия на развитие математики и физики, в том числе, на теорию устройства вселенной, которые сегодня даже невозможно предсказать.

Добавлено спустя 33 минуты 56 секунд:


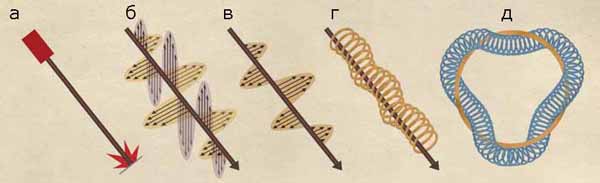
Геометрическая картина мира возникает из анализа его поведения. Простейший и наиболее известный пример – электрические и магнитные силы. Электрическая искра, магнитное притяжение, свет лазера представляют собой разные проявления электрических и магнитных полей, которые пронизывают все пространство. Физики полагают, что все в мире – силы природы и даже частицы материи – проявления полей различных типов. Поведение этих полей можно положить в основу построения некоей наглядной геометрической структуры

Луч лазера (а) состоит из осциллирующих электрического и магнитного полей (б), которые суть проявления одного поля – электромагнитного поля «связности» (в). В рамках рассматриваемого геометрического подхода это поле описывает, как круговой «слой», которому принадлежат электромагнитные взаимодействия, вращается вокруг луча. Этот круговой слой «присоединен» к каждой точке пространства–времени, и частица света (фотон) соответствует волнообразному движению этих окружностей (г). Заряженная частица (например, электрон) в таком геометрическом формализме соответствует другому слою, который оборачивается вокруг кругового слоя (д)

https://habr.com/ru/articles/117287/

[Око]

Гаррет Лиси о единой геометрической теории

phpBB [media]

Гаррет Лиси "Исключительно простая теория всего" (An Exceptionally Simple Theory of Everything) - это единая теория поля, предложенная американским физиком Гарретом Лиси в 2007 году. Она предполагает объединение всех фундаментальных взаимодействий на основе группы Ли типа E8.
Более подробно:
Теория Лиси, опубликованная 6 ноября 2007 года, стремится описать все известные физические взаимодействия, используя одну математическую структуру. В основе теории лежит группа Ли E8, которая, по мнению Лиси, является ключом к пониманию фундаментальной симметрии Вселенной. Некоторые физики, такие как Джон Бэйз, поддержали эту теорию.
Однако, теория Лиси также столкнулась с критикой и обнаружением неточностей. Несмотря на это, она остается важной вехой в поисках единой теории поля, над которой работали многие ученые, включая Альберта Эйнштейна.
Важно отметить, что "Теория всего" в контексте физики - это стремление найти единую теорию, которая объяснит все взаимодействия и частицы в природе. Существуют и другие подходы к этой проблеме, например, теория струн или петлевая квантовая гравитация.
В философии термин "теория всего" также используется для обозначения всеобъемлющей концепции, описывающей природу бытия.

[Око]

неожиданно почти согласна с этим товарищем по поводу глубинной математики.
Перельман, конечно, красава. То, что он сделал очень трудно осознать... да что там трудно - невозможно. так же как группу Е8.
даже Савватеев в одной из лекций признается, что не совсем понимает такую связь гомеоморфных пространств.
только последовательность абстрактных математических операций... или глубинная синхронизация.
но насчет перехода к практике - не вижу смысла. Если человек не готов, его не затащишь насильно в эти слои.
"В том, что я делаю, смысла не больше, чем в высеченной песчинке. ибо всё есть всё, и чем больше я погружаюсь туда, тем меньше я остаюсь собой" (с)

Перельман, Платоновы тела и многомерные символы

phpBB [media]

00:00:00 Введение
00:00:46 Глубинная математика
00:01:42 Волновая составляющая
00:01:59 Доказательство бесконечности
00:03:35 Ограниченность ума
00:04:05 Горизонтальное время
00:05:23 Элементали и волшебство
00:06:11 Технократические коды

[Око]

Сриниваса Рамануджан - Человек, который познал бесконечность (роман Роберта Каниджела и фильм 2015 года)

Он родился в небольшом городке в Индии 22 декабря 1887 г. Его семья была небогатой и принадлежала к касте браминов (священников, учителей и др.). Уже в 10 лет Рамануджан явно выделялся среди прочих по результатам экзаменов в обновленной системе школьного образования. Он также был известен из-за своей исключительной памяти: он мог декламировать цифры числа пи так же хорошо, как корни санскритских слов. Когда в возрасте 17 лет он закончил среднюю школу, ему дали стипендию для обучения в колледже.

Спойлер

В средней школе Рамануджан начал самостоятельно изучать математику и проводить собственное исследование численной оценки постоянной Эйлера и свойств чисел Бернулли. Ему повезло, что в 16 лет (в те дни, задолго до Интернета!) он получил копию удивительно хорошего и полного (по крайней мере, по состоянию на 1886 г.) конспекта по математике для студентов высшей школы, состоявшего из 1055 страниц! Книга была написана преподавателем трехлетней программы по математике для подготовки к экзаменам в Кембридж, и его скупой формат в стиле «только факты» был очень похож на тот, что Рамануджан использовал в своем письме к Харди.
Рамануджан переехал в Мадрас (теперь Ченнаи), где пробовал учиться в разных колледжах, болел и в результате продолжил свое независимое исследование по математике. В 1909 году, когда ему был 21 год, его мама в соответствии с обычаями того времени договорилась о его свадьбе с 10-летней девочкой по имени Янаки, которая начала жить с ним пару лет спустя.

Рамануджан обеспечивал себя, занимаясь репетиторством по математике, но вскоре он стал известен в окрестностях Мадраса как математик и начал печататься в недавно запущенном Журнале Индийского математического общества. Его первая статья, опубликованная в 1911 году, была посвящена вычислительным свойствам чисел Бернулли (те же числа Бернулли, что Ада Лавлейс (см. статью "Распутывая историю Ады Лавлейс (первого программиста в истории)" на Хабре) использовала в своей статье от 1843 года про аналитическую машину). Хотя его результаты не слишком впечатляли, подход Рамануджана был интересным и оригинальным: в нем сочетались непрерывная («каково численное значение?») и дискретная («какое разложение на простые множители?») математика.
После того, как друзьям-математикам Рамануджана не удается получить ему стипендию, он начинает искать работу, и в марте 1912 года Рамануджан попадает счетоводом в порт Мадрас. Его босс — главный бухгалтер — интересовался академической математикой и стал пожизненным его сторонником. Руководителем порта Мадрас в то время был выдающийся британский инженер-строитель, так что Рамануджан через него начал взаимодействовать с некоторыми британскими экспатриантами. Они рассуждали о том, есть ли у него «способности великого математика» или же он просто «мальчик-калькулятор». Они писали профессору Хилл в Лондон, который посмотрел на ряд диковинных заявлений Рамануджана о расходящихся рядах и заявил, что "г-н Рамануждан, очевидно, человек со вкусом к математике, и даже с некоторыми способностями, но он идет по неверному пути". Хилл предложил Рамануджану изучить некоторые книги.

В то время, как друзья Рамануджана продолжали искать способ поддержать его, он решил сам начать писать британским математикам — пускай и с некоторой помощью при составлении писем на английском языке. Мы не знаем точно, кому он написал первому, хотя давний соратник Харди Джон Литтлвуд незадолго до своей смерти 64 года спустя упомянул два имени: Х. Ф. Бейкер и Е. В. Хобсон. Они оба были не слишком удачным выбором: Бейкер работал в области алгебраической геометрии, а Хобсон занимался математическим анализом: достаточно далеко от того, что делал Рамануджан. В любом случае, ни один из них не ответил. Но на одно их писем ответил Харди.

Харди остроумно прокомментировал результаты, сообщённые ему Рамануджаном: «Они должны быть истинными, поскольку если бы они не были истинными, то ни у кого не хватило бы воображения, чтобы изобрести их». Его формулы иногда всплывают в современнейших разделах науки, о которых в его время никто даже не догадывался.
https://habr.com/ru/companies/wolfram/articles/306250/

Сам Рамануджан говорил, что формулы являлись ему во сне и внушались в молитве (в индуизме: в мантра-йоге, медитации) богиней Намагири Тхайяр (Махалакшми), почитаемой в Намаккале.
Чтобы сохранить наследие этого удивительного, ни на кого не похожего математика, в 1957 году Институт фундаментальных исследований Тата издал двухтомник с фотокопиями его черновиков.

Наука ничего не выиграла от того, что Кумбаконамский колледж отверг единственного большого учёного, которого он имел, и потеря была неизмеримой. Судьба Рамануджана — худший известный мне пример вреда, который может быть причинён малоэффективной и негибкой системой образования. Требовалось так мало, всего 60 фунтов стерлингов в год на протяжении 5 лет и эпизодического общения с людьми, имеющими настоящие знания и немного воображения, и мир получил бы ещё одного из величайших своих математиков…

https://ru.wikipedia.org/wiki/Сриниваса_Рамануджан